Introduction:

Over the years, I've written seven flight simulations. Looking back on them, I can see that each was written for a specific purpose. I love numerical modeling. Applying math and physics to a problem and working through a derivation to create a final model puts me in my natural habitat. Then I enjoy embodying that model in code and exercising it to get answers. For me, that's what Engineering is all about. The rigid body equations of motion, which all flight simulations are based on, are just such a system. When I first started writing flight simulations, I didn't fully understand them. In all of the texts I could find, the derivation of the equations was incomplete, with skipped steps and lots of confusing hand waving. In recent years, I've gone back, collecting as much as I could from disparate sources, and I now have the only complete derivation of the equations of motion that I've ever seen. It's liberating to finally understand them from front to back.

Naval Air Engineering Center:

The first flight simulation I wrote was in my first real engineering job, in the Advanced Systems Group at the Naval Air Engineering Center. We did a lot of Operations Research work in that branch, studying complex systems, creating techniques for analyzing them, and then improving or optimizing them. The paper at the right, written by our Branch Head and his Deputy, is a good example of that work. (Click on any image on this page to see a larger version.) As one of our analysis tools in the branch, I created a 3 degree-of-freedom flight simulation that predicted only the longitudinal motion of an aircraft. The dynamic model included catapult tow forces as well as constrained motion along a curved surface. Using it, we could analyze the requirements that different aircraft placed on the sizing and use of a catapult. We could also see the effect that a curved, ski-jump shaped, flight deck would have on the launch of any aircraft, and how its use could affect the size of the flight deck and the length of the catapult. Applying the program to foreign aircraft carriers, we could predict the size of the largest aircraft they could launch. I took the simulation with me to my next assignment, in the Research and Development Department. There, with some modifications, we used it to evaluate possible future aircraft/ship combinations, to determine whether aircraft carrier sizes could be reduced or mission effectiveness increased. I was very pleased to find the program still in use by the department a few years later. In its last incarnation--that I know of--I used the same simulation as the basis for a Visual Landing Aid design and analysis system. Combined with a pilot model and a random number generator, we could use the system to analyze aircraft carrier visual landing aids, generating touchdown point distributions along the arresting portion of the flight deck. That's a good amount of mileage from one simulation.

Naval Air Development Center

Later, I transferred to the Navy's Flight Dynamics Branch at the Naval Air Development Center. There, they used flight simulations for their most basic purpose--evaluating and improving aircraft flight dynamics, flying qualities and control harmony. They gave me the assignment to create a new simulation for the group. The simulation embodied a decoupled, 6 degree-of-freedom (3 DOF longitudinal, 3 DOF lateral/directional), linearized model. 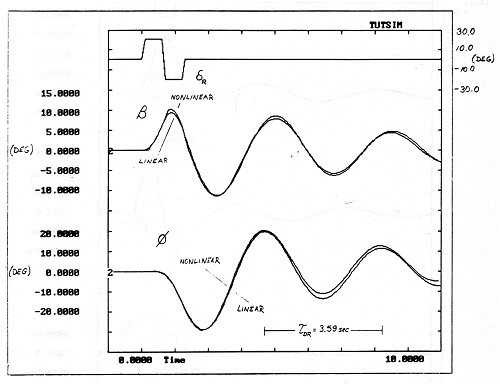They already had a coupled, 6 degree-of-freedom, non-linear simulation in the group, and they wanted this new model for comparison purposes. I wrote the report at the left on the new simulation, comparing its predictions with those of the non-linear model. The results were interesting. The linear model would match the non-linear model during a control deflection. But then, as one would expect, with increasing simulated time, the linear response would slowly diverge from the non-linear response. At the time that I wrote this simulation, the group was doing a lot of work with the McDonnel-Douglas T-45 Goshawk. The figure to the right shows one plot from the report: the T-45's response to a rudder doublet, as predicted by both models. Note the small differences in the responses and the increasing difference between the curves as time marches on.

My next flight simulation was for a very focused purpose. I joined a group that was creating the world's first fully autonomous UAV control system. For our work, we needed a hardware-in-the-loop (HIL) simulation. That kind of simulation is used to make a system think that it is connected to a real device. In our case, we wanted our airborne control system to think that it was flying in a real airplane. With the HIL simulation, we could develop and test the airborne control system in the lab, on the workbench. I created a 6 degree-of-freedom, non-linear flight simulation of the UAV, and added to it realistic dynamic models of a gimbal and camera. Written carefully, I found that the simulation could run many times faster than real-time on our 20 MHz PC. We eventually increased the realism of the simulation even more by adding models, generating realistic errors and noise, of the sensors and actuators on the aircraft. Even with those added, it still ran faster than real-time. Here is a paper that I wrote on the simulation for a computer programming conference and a video of the simulation in action:

The Sensor Driven Airborne Replanner Simulation

The Sensor Driven Airborne Replanner simulation being used for hardware-in-the-loop flight control system development.

Analytical Methods, Inc.

I recently wrote another hardware-in-the-loop simulation at Analytical Methods, Inc. That simulation was created for the laboratory development of their collapsible-wing, man-portable UAV. We had a full set of aerodynamic data for the aircraft, assembled from wind tunnel and CFD analyses. I wrote the simulation to sample that data at runtime, providing a fully nonlinear simulation that could reproduce the aircraft dynamics over the full range of airspeeds and attitudes, including departures from flight in the post-stall and spin regimes. Having never had a full aerodynamic data set to work with before, I was stunned by the realism of the simulation's responses.

Current Developments:

I'm currently creating a new flight simulation for my own use. I've included all of the lessons I've learned from developing past simulations and I can say that this is the best I've ever developed. The simulation is intended for many different uses, from open-loop, bare-airframe flight dynamics analyses to hardware-in-the-loop simulation. It assumes a round, rather than flat, Earth model and will correctly model a vehicle's dynamics from the surface up through orbit, so it can be used on aircraft or rockets. I've written the system so that new dynamic models, of gimbals, servos, engines, sensors, etc., can be added with very little effort. The program can communicate and be controlled by any other program, because its interface is the UDP stack. It will have a selection of "cabs" that can be used to operate the simulation, from the keyboard and joystick, from input files, from an A/D--D/A interface (for harware-in-the-loop work) or any others that prove useful. It will also have hooks to connect to FlightGear and X-Plane, for use as visualization systems. On my 2.13 GHz Pentium laptop, it currently runs about 2,000 times real-time. So it's perfect for use in developing intelligent systems, where full missions need to be flown or where many instances of the simulation (many aircraft, that is) need to be simulated at one time. The figure to the right is the output from a run controlled with the open-loop cab. Here, I'm simulating a Cessna 150 trimmed at an approach speed of 70 kts. A doublet input is applied to the rudder and then the aircraft is allowed to respond. In the "Body-Axis Velocities" plot, you can see the rudder input and the initial response of the aircraft, as the lateral velocity (v) oscillates and damps-out quickly. In the "Body-Axis Rotational Rates" and "Lateral/Directional Displacements" plots, you can see the "dutch roll" response of the aircraft, as motion around the vertical axis is linked to the motion about the roll axis. Aircraft "heading" angle is labeled "Psi", bank angle is labeled "Phi" and sideslip angle is labeled "Beta". The dutch roll damps-out quickly, which is a positive attribute for an aircraft, especially a trainer. After the dutch roll damps out, the aircraft enters into a spiral mode, as it rolls from the upright, accelerates and begins descending. This mode would be dangerous if the airplane were allowed to fly without any control input. But with a pilot at the controls it's not an issue. The spiral mode diverges so slowly that the pilot will correct for it without even knowing that it's happening.

I'll be using this simulation to create new UAV control systems. If you'd like to use it for your work, I intend to offer copies of the simulation for sale after it's complete. Stay tuned.